Domene

Pri interpretaciji izrazov nismo omenjali rekurzije. Spomnimo se, da jo lahko uvedemo z izrazom \(\kwdpre{rec} f \, x . M\), za katerega velja

\[ \infer{}{ (\kwdpre{rec} f \, x . M) \, V \leadsto M[V / x, (\kwdpre{rec} f \, x . M) / f] } \]

Če bi želeli skladnost denotacijske semantike z operacijsko, bi torej moralo veljati

\[ \itp{(\kwdpre{rec} f \, x . M)}(\itp{V}) = \itp{M}(\itp{V}, \itp{\kwdpre{rec} f \, x . M}) \]

Na primer, če za \(M\) vzamemo \(x + \intsym{1}\), za \(V\) pa \(\intsym{0}\), dobimo

\[ \itp{(\kwdpre{rec} f \, x . f \, x + \intsym{1}) \, \intsym{0}} = \itp{(\kwdpre{rec} f \, x . f \, x + \intsym{1}) \, \intsym{0}} + 1 \]

kar seveda ni res. V splošnem pa nam enačba pove, da ima (malo preurejeni) \(\itp{M}\) vedno fiksno točko. To za množice in preslikave med njimi seveda ne velja. Smo pa fiksne točke že konstruirali v poglavju o indukciji, kjer smo imeli monotono preslikavo na množicah \(F\), ki smo jo iterirali na prazni množici \(\emptyset\), da smo dobili množico \(I = \bigcup_{n = 0}^{\infty} F^i(\emptyset)\), za katero je veljalo \(F I = I\). Podoben postopek želimo narediti v splošnem, kar nas pripelje do definicije domen.

Domene

Zaporedje \((x_i)_{i \in \mathbb{N}}\) v delno urejeni množici \(D\) je veriga, če za vsak \(i \in \mathbb{N}\) velja \(x_i \le x_{i + 1}\).

Delno urejena množica \((D, \le)\) je domena, če:

• obstaja najmanjši element \(\bot_D\), ki ga imenujemo dno, za katerega velja \(\bot_D \le x\) za vsak \(x \in D\).

• ima vsaka veriga \((x_i)_i\) natančno zgornjo mejo, ki jo označimo z \(\bigvee_i x_i\).

Primeri domen so:

• Interval \([0, 1]\) ali pa \([0, 1) \cup \{2\}\) z običajno urejenostjo \(\le\). Interval \((0, 1]\) ni domena, ker nima dna, interval \([0, 1)\) pa ne, ker veriga \((1 - \frac{1}{i + 1})_i\) nima supremuma.

• Vsako množico \(A\) lahko razširimmo z dodatnim elementom \(\bot\). Na \(A_\bot = A + \{ \bot \}\), lahko definiramo urejenost \(\le\) kot \(x \le y \iff x = \iota_2(\bot) \lor x = y\). Pri zapisu elementov nismo pedantni, ampak namesto \(\iota_1(a)\) pišemo kar \(a\), namesto \(\iota_2(\bot)\) pa kar \(\bot\). Primer dvigov sta domeni \(\mathbb{B}_\bot\) ali \(\mathbb{Z}_\bot\), ki ju bomo še uporabljali in sta videti kot

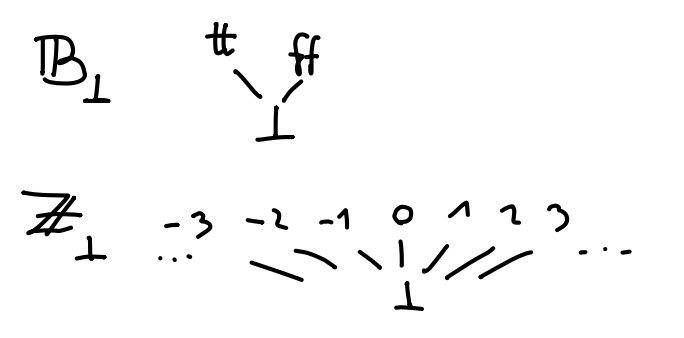
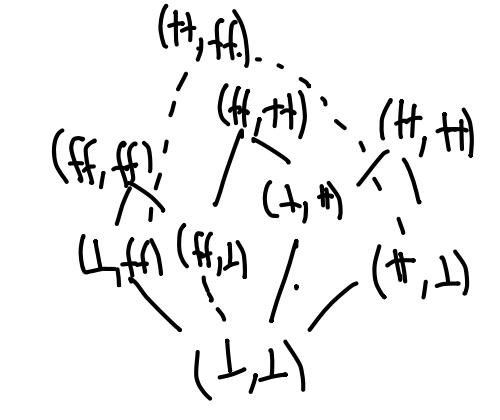
Za poljubni domeni \((D_1, \le_1)\) in \((D_2, \le_2)\) lahko na kartezičnem produktu \(D_1 \times D_2\) definiramo urejenost

\[ (x_1, x_2) \le (y_1, y_2) \iff x_1 \le_1 y_1 \land x_2 \le_2 y_2 \]

Preverimo lahko, da res dobimo domeno, ki ima za dno par \((\bot_{D_1}, \bot_{D_2})\). Skica domene \(\mathbb{B}_\bot \times \mathbb{B}_\bot\) je

Vzemimo domeni \((D_1, \le_1)\) in \((D_2, \le_2)\). Pravimo, da je preslikava \(f : D_1 \to D_2\) zvezna, če:

• je monotona, torej iz \(x \le_1 y\) sledi \(f(x) \le_2 f(y)\), in

• ohranja supremume verig, torej je \(f(\bigvee_i x_i) = \bigvee_i f(x_i)\) za vsako verigo \((x_i)_i\).

Pri tem desni supremum obstaja, ker je \(f\) monotona, zato je \((f(x_i))_i\) veriga v \(D_2\).

Trditev. Vzemimo domene \((D_1, \le_1)\), \((D_2, \le_2)\) in \((D_3, \le_3)\) ter zvezni preslikavi \(f : D_1 \to D_2\) in \(g : D_2 \to D_3\). Tedaj je \(g \circ f : D_1 \to D_3\) zvezna preslikava.

Dokaz. Preveriti moramo monotonost in ohranjanje supremumov:

• Naj bo \(x \le_1 y\). Ker je \(f\) monotona, velja \(f(x) \le_2 f(y)\), zaradi monotonosti \(g\) pa še \(g(f(x)) \le_3 g(f(y))\).

• Vzemimo verigo \((x_i)_i\). Tedaj je

\[(g \circ f)(\bigvee_i x_i) = g (f (\bigvee_i x_i)) = g (\bigvee_i f(x_i)) = \bigvee_i g(f(x_i))\]

■

Domene in zvezne preslikave zadoščajo lastnosti, ki jo potrebujemo za interpretacijo rekurzije: vsaka zvezna preslikava ima fiksno točko.

Izrek (Tarski). Naj bo \((D, \le)\) domena in \(f : D \to D\) zvezna preslikava. Tedaj ima \(f\) najmanjšo fiksno točko, ki jo označimo s \(\mathrm{fix} \, f\).

Dokaz. Vzemimo zaporedje \((x_i)_i\), definirano z \(x_i = f^i(\bot)\). Ker je \(x_0 = \bot \le f(\bot) = x_1\) in je \(f\) monotona, lahko z indukcijo pokažemo, da je \((x_i)_i\) veriga. Pokažimo, da je njen supremum \(x = \bigvee_i x_i\) najmanjša fiksna točka preslikave \(f\). Zaradi zveznosti \(f\) velja

\[ f(x) = f(\bigvee_i x_i) = \bigvee_i f(x_i) = \bigvee_i x_{i + 1} = x \]

saj dobimo isto verigo, le premaknjeno za en člen. Torej je \(x\) fiksna točka \(f\). Naj velja tudi \(f(y) = y\). Ker je \(x_0 = \bot \le y\), po indukciji velja tudi \(x_{i + 1} = f(x_i) \le f(y) = y\) za vse \(i\). Ker je celotna veriga pod \(y\), je pod \(y\) tudi supremum, torej \(x \le y\). ■

Tako kot smo prej tipe interpretirali z množicami, izraze pa s preslikavami med njimi, lahko vidimo, da bomo zdaj tipe interpretirali z domenami, izraze pa z zveznimi preslikavami. Za to najprej potrebujemo domeno, s katero bomo interpretirali funkcijski tip.

Vzemimo domeni \((D_1, \le_1)\) in \((D_2, \le_2)\). Na podmnožici vseh zveznih preslikav \(f : D_1 \to D_2\) definiramo ureditev

\[ f \le g \iff \forall x \in D_1. f(x) \le_2 g(x) \]

Preverimo lahko, da dobimo domeno, ki jo imenujemo domena zveznih preslikav in jo označimo z \([D_1 \to D_2]\). Pri dokazu potrebujemo sledečo lemo.

Lema. Vzemimo dvojno zaporedje \(x_{ij}\) v \(D\), da velja \(x_{ij} \le x_{i' j'}\) za vse \(i \le i'\) in \(j \le j'\). Tedaj velja

\[\bigvee_i \bigvee_j x_{ij} = \bigvee_j \bigvee_i x_{ij} = \bigvee_k x_{kk}\]

Dokaz. Ker za poljubna \(i\) in \(j\) velja \(x_{ij} \le x_{\max(i, j) \max(i, j)} \le \bigvee_k x_{kk}\), za poljuben \(i\) velja \(\bigvee_j x_{ij} \le \bigvee_k x_{kk}\) in zato tudi \(\bigvee_i \bigvee_j x_{ij} \le \bigvee_k x_{kk}\). Obratno za poljuben \(k\) velja \(x_{kk} \le \bigvee_j x_{kj} \le \bigvee_i \bigvee_j x_{ij}\) torej dobimo neenakost tudi v drugo smer, zato velja \(\bigvee_i \bigvee_j x_{ij} = \bigvee_k x_{kk}\). Druga enakost velja zaradi simetrije. ■

Trditev. V domeni zveznih preslikav obstajajo supremumi poljubnih verig.

Dokaz. Vzemimo verigo \((f_i)_i\) v domeni zveznih preslikav \([D_1 \to D_2]\) in pokažimo, da ima supremum. Definirajmo funkcijo \(f\) s predpisom \(f(x) = \bigvee_i f_i(x)\). Ker je \((f_i)_i\) veriga, je veriga tudi \((f_i(x))_i\), zato je preslikava dobro definirana. Pokažimo, da je funkcija \(f\) tudi zvezna. Vzemimo verigo \((x_j)_j\). Tedaj velja

\[ f\big(\bigvee_j x_j\big) = \bigvee_i f_i\big(\bigvee_j x_j\big) = \bigvee_i \bigvee_j f_i(x_j) = \bigvee_j \bigvee_i f_i(x_j) = \bigvee_j f(x_j) \]

pri čemer smo uporabili definicijo \(f\), zveznost \(f_i\) ter lemo od prej. Tako velja \(f \in [D_1 \to D_2]\), pokazati pa moramo le še, da je \(f\) res supremum verige \((f_i)_i\).

Ker za poljubna \(x\) in \(i\) velja \(f_i(x) \le \bigvee_i f_i(x) = f(x)\), je \(f\) res zgornja meja verige \((f_i)_i\). Naj bo \(g\) zgornja meja verige \((f_i)_i\). Če za vsak \(i\) velja \(f_i \le g\), tedaj za vsak \(x\) velja \(f_i(x) \le g(x)\) in je zato \(f(x) = \bigvee_i f_i(x) \le g(x)\), torej je tudi \(f \le g\), s čimer je \(f\) res supremum verige \((f_i)_i\). ■

Interpretacije tipov in izrazov

Zdaj lahko ponovimo celotno zgodbo od prej. Za vsak tip \(A\) definiramo njegovo interpretacijo \(\itp{A}\), ki je domena, rekurzivno definirana kot:

\[\begin{split} \begin{align*} \itp{\boolty} &= \mathbb{B}_\bot \\ \itp{\intty} &= \mathbb{Z}_\bot \\ \itp{A \to B} &= [\itp{A} \to \itp{B}] \end{align*} \end{split}\]

Podobno definiramo interpretacijo kontekstov kot

\[ \itp{x_1 : A_1, \dots, x_n : A_n} = \itp{A_1} \times \dots \times \itp{A_n} \]

saj vemo, da je tudi produkt domen domena. Izraza \(\Gamma \vdash M : A\) bomo interpretirali z zveznimi preslikavami

\[ \itp{\Gamma \vdash M : A} : \itp{\Gamma} \to \itp{A} \]

ki so podane s sledečimi predpisi:

\[\begin{split} \begin{align*} \itp{\Gamma \vdash x_i : A_i}(a_1, \dots, a_n) &= a_i \\ \itp{\Gamma \vdash \true : \boolty}(\gamma) &= \ttt \\ \itp{\Gamma \vdash \false : \boolty}(\gamma) &= \fff \\ \itp{\Gamma \vdash \ifthenelse{M}{M_1}{M_2} : A}(\gamma) &= \begin{cases} \itp{M_1}(\gamma) & \itp{M}(\gamma) = \ttt \\ \itp{M_2}(\gamma) & \itp{M}(\gamma) = \fff \\ \bot & \itp{M}(\gamma) = \bot \end{cases} \\ \itp{\Gamma \vdash \intsym{n} : \intty}(\gamma) &= n \\ \itp{\Gamma \vdash M_1 + M_2 : \intty}(\gamma) &= \itp{M_1}(\gamma) +_\bot \itp{M_2}(\gamma) \\ \itp{\Gamma \vdash M_1 * M_2 : \intty}(\gamma) &= \itp{M_1}(\gamma) \cdot_\bot \itp{M_2}(\gamma) \\ \itp{\Gamma \vdash M_1 < M_2 : \boolty}(\gamma) &= \itp{M_1}(\gamma) <_\bot \itp{M_2} \\ \itp{\Gamma \vdash \lambda x. M : A \to B}(\gamma) &= a \mapsto \itp{\Gamma, x : A \vdash M : B}(\gamma, a) \\ \itp{\Gamma \vdash M_1 \, M_2 : B}(\gamma) &= \big(\itp{M_1}(\gamma)\big)\big(\itp{M_2}(\gamma)\big) \\ \itp{\Gamma \vdash \kwdpre{rec} f \, x . M : A \to B}(\gamma) &= \mathrm{fix} (f \mapsto (a \mapsto \itp{M}(\gamma, f, a))) \end{align*} \end{split}\]

kjer je \(+_\bot : \mathbb{Z}_\bot \times \mathbb{Z}_\bot \to \mathbb{Z}_\bot\) definiran kot

\[ m +_\bot n = m + n \qquad \bot +_\bot n = m +_\bot \bot = \bot +_ \bot \bot = \bot \]

in podobno za \(\cdot_\bot\) in \(<_\bot\). Za vse preslikave moramo še preveriti, da so zvezne. Za primer poglejmo, da je zvezna preslikava \(\mathrm{fix} : [D \to D] \to D\). Poleg monotonosti moramo preveriti, da velja \(\mathrm{fix} \bigvee_i f_i = \bigvee_i \mathrm{fix} f_i\) za poljubno verigo preslikav \((f_i)_i\). Vemo, da velja \((\mathrm{fix} g) = \bigvee_j g^j(\bot)\), zato lahko izračunamo:

\[\begin{split} \begin{align*} (\mathrm{fix} \bigvee_i f_i) &= \bigvee_j (\bigvee_i f_i)^j (\bot) \\ &= \bigvee_j (\bigvee_i f_i^j(\bot)) \\ &= \bigvee_i (\bigvee_j f_i^j(\bot)) \\ &= \bigvee_i (\mathrm{fix} f_i) \end{align*} \end{split}\]

saj lahko z indukcijo na \(j\) pokažemo, da zaradi zveznosti \(f_i\) velja \((\bigvee_i f_i)^j(x) = \bigvee_i f_i^j(x)\) za poljuben \(x\).